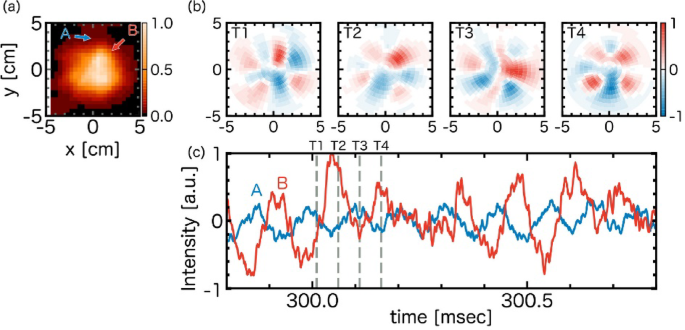
Plasma is a non-equilibrium system of strong nonlinearity that provides rich phenomena for modern physics. One such physical topic is the roles of fluctuations and turbulence in the structural formation and dynamics of plasmas. Particularly, in the research of magnetically confined plasmas, various phenomena associated with turbulence have been found and investigated, especially in the research of magnetized plasma for realizing a nuclear fusion reactor. The phenomena include the non-local transport1,2,3,4,5,6 the global linkage of the turbulent activity7,8,9turbulence spreading and avalanche10,11,12,13,14,15,16which are thought to be caused by nonlinear interactions between disparate scale fluctuations covering the entire plasma17,18. The investigation of these phenomena needs simultaneous and entire cross-sectional observation of the turbulence field that often shows symmetry breaking characteristics19,20.
Tomography is a possible candidate, amongst various plasma diagnostics, to achieve the entire measurement of plasma. To confirm the capability of tomography as a tool for turbulence field measurement, a prototype system has been installed in a cylindrical device called Plasma Assembly for Nonlinear Turbulence Analysis (PANTA). The tomography system successfully demonstrates its feasibility for the entire field observation of plasma turbulence in space and time21,22. Moreover, various analyzing tools for tomographic images have been developed to extract the two-dimensional feature of the fluctuations, such as Fourier-Bessel Function analysis, Fourier Rectangular Function (FRF) analysis23modal polarization analysis24,25 and so on26.
Recently, the advanced use of the FRF analysis has been proposed27,28and the proposed analysis have been applied to an oscillatory state dominated by mother (M) mode (m = 4 mode) in PANTA plasma29. The analysis revealed that the oscillatory state repeats transition quasi-periodically to two phases distinguished by the strength in nonlinear modal coupling of M (m = 4) mode with father (F) mode (m = 1 mode). Moreover, the analyses disclose an important role of F (m = 1) mode dynamics for the phase transitions. This article presents the advanced analysis using FRF as a tool to investigate the physics of plasma turbulence, with emphasis on the excellent capabilities of the FRF analysis in its applicability on the cylindrical system and to show intriguing results of its application as an example to reveal the fundamental processes and spatiotemporal behaviors of modal structure and couplings in an oscillatory state in a cylindrical plasma.
Fourier-rectangular function (FRF) analysis
The FRF series is used to expand a two-dimensional image of plasma emission intensity, \(\:\epsilon\:\left(r,\theta\:,t\right),\) on a cylindrical coordinate. The FRF expansion of the emission intensity is defined as follows,
$$\varepsilon \left( {r,\theta ,t} \right)=\mathop \sum \limits_{n} {a_{n,0}}\left( t \right)\frac{{{R_n}\left( r \right)}}{{\sqrt 2 }}+\mathop \sum \limits_{n} \mathop \sum \limits_{{m>0}} {R_n}\left( r \right)\left[ {{a_{n,m}}\left( t \right)\cos \left( {m\theta } \right)+{b_{n,m}}\left( t \right)\sin \left( {m\theta } \right)} \right].$$
(1)
Where \(\:n\) and \(\:m\) represent the radial position and azimuthal mode number, respectively. \(\:{R}_{n}\left(r\right)\) is the function that has a finite value in a radial range from \(\:r={r}_{n}-{\delta\:}_{r}\) to \(\:r={r}_{n}+{\delta\:}_{r}\). Supposing that the functions, \(\:{\varphi\:}_{l}\left(r,\:\theta\:\right)\), are the orthogonal bases for FRF expansion, that is, \(\:{\varphi\:}_{l}\left(r,\:\theta\:\right)=\frac{{R}_{n}\left(r\right)}{\sqrt{2}}\), \(\:{\varphi\:}_{l}\left(r,\:\theta\:\right)={R}_{n}\left(r\right)\text{cos}\left(m\theta\:\right)\) or, \(\:{\varphi\:}_{l}\left(r,\:\theta\:\right)={R}_{n}\left(r\right)\text{sin}\left(m\theta\:\right)\), where the suffix, \(\:l\), is renumbered from the set of the integers, \(\:(n,m)\), in an appropriate order, they satisfy the orthonormal relationship as follows,
$${\delta _{{l_1},{l_2}}}=\smallint {\phi _{{l_1}}}\left( {r,\theta } \right)~{\phi _{{l_2}}}\left( {r,~\theta } \right)rdrd\theta.$$
(2)
where \(\:{\delta\:}_{{l}_{1},{l}_{2}}\) represents Kronecker’s delta. The FRF coefficients are obtained using the following formula,
$$\:{a}_{n0}\left(t\right)=\int\:\epsilon\:\left(r,\theta\:,t\right)\frac{{R}_{n}\left(r\right)}{\sqrt{2}}rdrd\theta\:,\:$$
$$\:{a}_{n,m}\left(t\right)=\int\:\epsilon\:\left(r,\theta\:,t\right){R}_{n}\left(r\right)\text{cos}\left(m\theta\:\right)rdrd\theta\:,\:$$
$$\:{b}_{n,m}\left(t\right)=\int\:\epsilon\:\left(r,\theta\:,t\right){R}_{n}\left(r\right)\text{sin}\left(m\theta\:\right)rdrd\theta\:.$$
By making a complex variable of the FRF coefficients, \(\:{c}_{n,m}\left(t\right)={a}_{n,m}\left(t\right)+\sqrt{-1}{b}_{n,m}\left(t\right)\), its absolute value and argument allows us to evaluate the local power and amplitude of each azimuthal mode structure, \(\:{P}_{m}\left({r}_{n},\:t\right)={\left|{c}_{n,m}\left(t\right)\right|}^{2}\), and \(\:{A}_{m}\left({r}_{n},\:t\right)=\sqrt{{P}_{m}\left({r}_{n},\:t\right)}\), respectively, and declination of the azimuthal mode, \(\:{\theta\:}_{n,m}\left(t\right)=\text{a}\text{r}\text{g}\left({c}_{n,m}\left(t\right)\right)\), as a function of radius. Also, the FRF complex coefficients can be used to quantify the tilt of the modal structure by taking the difference of the declination between neighboring radial bands, \(\:{\Delta\:}{\theta\:}_{n,m}=\text{arg}\left({c}_{n+1,m}{c}_{n,m}^{*}\right)\), where \(\:{c}_{n,m}^{*}\left(t\right)\) represents the conjugate of the complex variable \(\:{c}_{n,m}\left(t\right)\). The FRF analysis is regarded as Fourier function series expansion in azimuthal coordinate defined on a radial band and allows easy extraction of modal properties of cylindrical plasmas at radially localized position, since the azimuthal structure is expressed using the traditional Fourier function expansion on individual radial bands. This feature of the FRF analysis is one of the advantages to other methods such as the Fourier-Bessel function expansion that treats azimuthal modes in a global property in the entire plasma region. By utilizing the properties, we propose newly extended FRF usages, namely FRF structural and modal coupling function analyses, to extract the spatiotemporal structure and dynamics from the 2D imaging data. Hereafter, the cartesian coordinate \(\:(x,\:y)\) is used to infer the local property of emission intensity or its fluctuation, and the cylindrical coordinate \(\:(r,\:\:\theta\:)\) is used to express the radial profile of azimuthally averaged emission intensity or fluctuation property.
FRF structural function: The structural function is introduced to evaluate the spatial pattern of each mode and its robustness. The structural function is defined as follows,
$${\alpha _m}\left( {{r_i},~{r_j},~\tau } \right)=\frac{{\left\langle {{c_{i,m}}\left( {t+\tau } \right)c_{{j,m}}^{*}\left( t \right)} \right\rangle }}{{\left\langle {\left| {{c_{i,m}}\left( {t+\tau } \right)} \right|} \right\rangle \left\langle {\left| {c_{{j,m}}^{*}\left( t \right)} \right|} \right\rangle }}.$$
(3)
where \(\:<>\) means the temporal average, \(\:〈a\left(t\right)〉=\frac{1}{T}{\int\:}_{{t}_{s}}^{{t}_{s}+T}a\left(t\right)dt\). The suffixes, i, j, represent the corresponding radial position \(\:{r}_{i}\) and \(\:{r}_{j}\). Here the parameter, \(\:{\alpha\:}_{m}\), is termed structural function, which can be divided into two variables: structural coherence, \(\:{\gamma\:}_{m}=\left|{\alpha\:}_{m}\right|\), and tilt angle between two positions, \(\:{\theta\:}_{i,j,m}\left({r}_{i},\:{r}_{j},\:\tau\:\right)=\text{a}\text{r}\text{g}\left({\alpha\:}_{m}\left({r}_{i},\:{r}_{j},\:\tau\:\right)\right)\). The FRF expansion is particularly powerful to analyse systems of cylindrical symmetry. Based on the FRF expansion, the structural function has an advantage to evaluate rigidness of radial structure for each azimuthal mode. In other words, how radial structure of fluctuations is stable in space and time.
FRF modal coupling function
The modal coupling function is defined as a triple product of the FRF coefficients as follows,
$${\beta _{m,n}}\left( {{r_i},~{r_j},~\tau } \right)=\frac{{\left\langle {{c_{i,m}}\left( {t+\tau } \right){c_{i,n}}\left( {t+\tau } \right)c_{{j,m+n}}^{*}\left( t \right)} \right\rangle }}{{\left\langle {\left| {{c_{i,m}}\left( {t+\tau } \right){c_{i,n}}\left( {t+\tau } \right)} \right|} \right\rangle \left\langle {\left| {c_{{j,m+n}}^{*}\left( t \right)} \right|} \right\rangle }}.$$
(4)
where \(\:\left|{\beta\:}_{m,n}\right|\) and \(\:\text{a}\text{r}\text{g}\left({\beta\:}_{m,n}\right)\) are termed the coupling power and the coupling angle, respectively, correspondingly to the squared bicoherence and bi-phase in Fourier analysis. The modal coupling function analysis provides a method to clarify the nonlinear coupling in time, different from the bicoherence analysis performed on frequency domain. Thus, the analysis can show the temporal evolution on real space, or spatial propagation of modal couplings in real space and time. The presented analysis result on the oscillatory state below is a good example which succeeds in revealing hidden processes occurring in its phase transitions, with the hidden dynamics of F (m = 1) mode.