Testing the feasibility of multi-modular design in an HTR-PM nuclear plant

The process and equipment design of multi-modular NPPs is nearly the same as that of single modular NPPs. The major difference between the multi-modular and single modular NPPs focuses on the control and operation that is mainly provided by the CCS. The multi-modular coordinated control is the mechanism playing a central role in the realization of multi-modular scheme, giving the plant responses in normal and abnormal scenarios. In this section, the coordination mechanism inside a single reactor module and between two modules are proposed, giving the CCS design of HTR-PM plant.

Coordinated control of a single reactor module

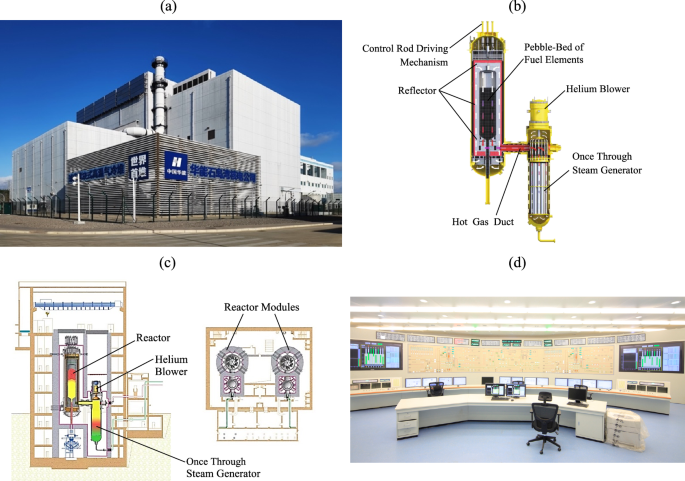
As illustrated in Fig. 2, the cold helium is first pressurized by the helium blower, before being directed to the reactor along the annular cold gas duct. Once it is blended within the bottom region of the reactor, the cold helium ascends through the boreholes in the side reflector from to the upper section, subsequently circulating downwards through the pebble-bed reaching temperatures near 700  °C at the pebble bed’s outlet¹⁸. The bypassed cold helium is collected and combined with the hot helium flowing from the pebble-bed inside the hot gas plenum located in the bottom reflector. The mixed hot gas, exceeding 550  °C, is guided to the primary side of OTSG via the hot gas duct, transforming the secondary feedwater flow to the superheated steam flow. The coordinated control within a reactor module is designed to regulated the tightly coupled process variables including neuron flux, helium temperature and steam temperature of an individual mHTGR module, ensuring the closed-loop stability in the scenarios of power-level maintaining and maneuvering. Similar to^36,37,38, the dynamic model of a reactor module for control design can be written as:

where P₀ is the rated thermal power of reactor, Λ is the prompt neutron generation time, λ is the averaged decay constant of delayed precursors, β is the fraction of delayed neutrons, n_r is the normalized neutron flux, c_r is the normalized concentration of delayed neutron precursors, G_r is the control rod differential worth, z_r is the total displacement of control rods, v_r is the control rod speed, T_R is the average temperature of reactor core with T_R,m as its initial steady value, α_R is the reactivity feedback coefficient of reactor core temperature, T_H is the average primary helium temperature, T_S is the average secondary coolant temperature of the steam generator, T_Sin is the coolant temperature at the secondary inlet of steam generator, M_S is the secondary heat capacity flow, μ_R, μ_H and μ_S are the total heat capacities of reactor core, primary helium and secondary coolant respectively, Ω_P and Ω_S are respectively the heat transfer coefficient between the helium and pebble-bed and that between the two sides of steam generator.

Define δn_r = n_r–n_r0, δc_r = c_r–c_r0, δρ_r = ρ_r–ρ_r0, δT_R = T_R–T_R0, δT_H = T_H–T_H0, δT_S = T_S–T_S0 and δT_Sin = T_Sin–T_Sin0, where n_r0, c_r0, ρ_r0, T_R0, T_H0, T_S0 and T_Sin0 are the setpoints of process variables n_r, c_r, ρ_r, T_R, T_H, T_S and T_Sin respectively. In addition, as δT_Sin is determined by the operational state of the conventional island, it is assumed that δT_Sin = 0 in the coordinated control design. Moreover, since the helium flowrate can be adjusted by the rotation rate of the primary helium blower, it is not loss of generality to assume that

where δG_P is the variation of the primary helium flowrate with respect to the setpoint, Ω_S0 is the value of heat transfer coefficient Ω_S at the concerned setpoint, Λ_S is a positive constant given by

with G_P0 being the setpoint of primary helium flowrate.

Further, define

and then the nonlinear state-space model for control design can be written as

where

x and ξ are state-variables, u is the control input, and y is the measurement output. The following proposition gives the output-feedback coordinated control of a single reactor module, and the corresponding sufficient condition for globally asymptotic closed-loop stability.

Proposition 1

Consider nonlinear system (7) giving the dynamics of a mHTGR-based reactor module. The output feedback control given by

guarantees globally asymptotic closed-loop stability, if inequalities

are all well satisfied, where \({\bar{k}}_{{\rm{P3}}}={k}_{{\rm{P3}}}+1\), \({\delta }_{\gamma }=\gamma -{\bar{k}}_{{\rm{P3}}}\),and control gains k_Pi, k_Dj, k_I3 and κ_i are all given postive constants (i = 1, 2, 3, and j = 1, 2).

Remark 1

By incorporating terms of x₄ and its time-derivative into setpoint n_r0, reactor control u₁ in (11) can be implemented in a cascaded manner shown in Fig. 3. Steam temperature control u₂ in (11) together with G_P0 gives the final setpoint of helium flowrate, which is further controlled by regulating the rotation rate of helium blower. The steam temperature control u₂ and helium flowrate control is also synthesized in a cascaded manner shown in Fig. 3. In addition, the inertia of helium blower can be compensated by enlarging gain k_P3 in control law (11). As the difference between the dynamics of mHTGR module and that of other type reactor modules is limited, coordinated control (11) for a single mHTGR module is referenceable to the control other types of reactor modules.

Coordinate control method between two reactor modules

From Fig, 2, the two reactor modules are coupled by the common secondary loop system. The main coupling hydraulic dynamics in normal operation scenario can described by the fluid flow network (FFN) shown in Fig. 9, where branches f₁ and f₂ are the pump branches of #1 and #2 reactor modules composed of a feedwater pump and a high pressure heater (HPH), branches 1 and 2 are the feedwater the OTSG secondary sides of #1 and #2 modules respectively, and branch 3 is the fluid branch including the turbine, condenser, low pressure heaters (LPHs) and deaerator. The branches denoted by solid line constitute a tree of this FFN, while the branches denoted by dashed line are the links forming a co-tree. Nodes n₁ and n₂ represents the outlets of #1 and #2 HPHs respectively, node n₃ is the inlet of common main steam header, node n₄ represents the outlet of deaerator. The feedwater flowrates of #1 and #2 modules can be described by the flowrates of branches 1 and 2 respectively, and the main steam pressure can be represented by the pressure drop of tree branch 3.

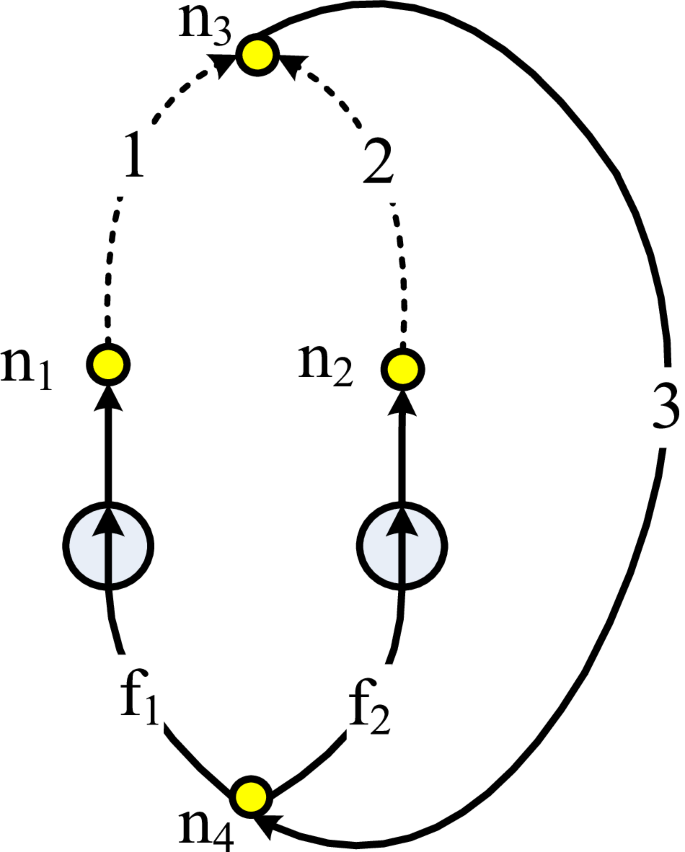
n₁, n₂, n₃ and n₄: nodes, f₁ and f₂: fan branches, branches 1 and 2: links, branches 3, f₁ and f₂: tree branches.

Based on the fluid dynamics of pipelines, the flowrates in branches 1, 2 and 3 can be governed by

where Q = [Q₁ Q₂ Q₃]^T, H = [H₁ H₂ H₃]^T, Q_D = [Q₁² Q₂² Q₃²]^T, L=diag([L₁ L₂ L₃]^T), R=diag([R₁ R₂ R₃]^T), Q_i, H_i, R_i and L_i are respectively the flowrate, pressure-drop, fluid resistance and fluid inertia of branches i (i = 1, 2, 3). In addition, the pressure-drops of pump branches f_k (k = 1, 2), i.e. H_fk can be given by

where H_dk is the pressure header provided by #k pump being proportional to the square of rotation rate, R_fk is the resistance coefficient of pump branch f_k, k = 1, 2.

By applying Kirchhoff’s current law (KCL) to node n₃, it can be seen that

giving that

Substitute (16) to (19),

Then, apply Kirchhoff’s voltage law (KVL) to the fundamental loops,

From (17), (20) and (21), one can see that

where L = L₁L₂L₃/(L₁L₂ + L₂L₃ + L₃L₁).

From (16), (22) and (23), the FFN dynamics is governed by nonlinear differential-algebraic system (DAS)

where Q_c = [Q₁ Q₂]^T, H_d = [H_d1 H_d2]^T, Q_cD = [Q₁² Q₂²]^T, R_c = diag([R₁ R₂]^T), R_f = diag([R_f1 R_f2]^T), L_c = diag ([L₁ L₂]^T), η = [1 1]^T. From Fig. 1, the operation of two reactor modules can be decoupled if the feedwater flowrates are well regulated, and the main steam pressure is firmly stabilized, giving that the coordinated control between two modules is essentially the flowrate-pressure joint control of the FFN shown in Fig. 9. The flowrate-pressure joint control design can be further transferred to the control design of nonlinear DAS (24), and the following proposition gives an adaptive control for system (24) with the sufficient condition for globally asymptotical closed-loop stability.

Proposition 2

Consider nonlinear DAS (24) with Q_cr = [Q_1r Q_2r]^T and H_3r being defined as the setpoints of Q_c and H₃ respectively. The joint controller

with \({\hat{{\bf{H}}}}_{{\rm{dr}}}\) and \({\hat{R}}_{3{\rm{r}}}\) given by adaptation law

provides globally asymptotic stability to setpoints if inequality

is well satisfied, where Q_ce = Q_c–Q_cr, H_3e = H₃–H_3r, Q_3r = Q_1r + Q_2r, Ω_i = R_i(Q_i+Q_ir) with i = 1, 2, 3, Ω_c = diag([Ω₁, Ω₂]^T), both Γ_a and Π_a are given positive constants, and Γ_d, Π_d and Λ_a are given positive-definite diagonal matrices.

Remark 2

It can be seen from (25) that the pressure header provided by #k pump are used to regulate the feedwater flowrate of #k reactor module (k = 1, 2), while the fluid resistance of tree branch such as the regulating value of turbine is applied for stabilizing the main stream pressure. Submit (26) to (25),

showing that the adaptive control laws are essentially distributed proportional-integral (PI) control algorithms. The two PI laws in (28) form the feedwater flowrate controllers of two modules and the main steam pressure controller shown in Fig. 3. Since the multiple reactor modules in a multi-modular NPP are coupled together by the common secondary FFN, coordinated control (28) can be also applicable to the coordination between all types of reactor module generating superheated steam.