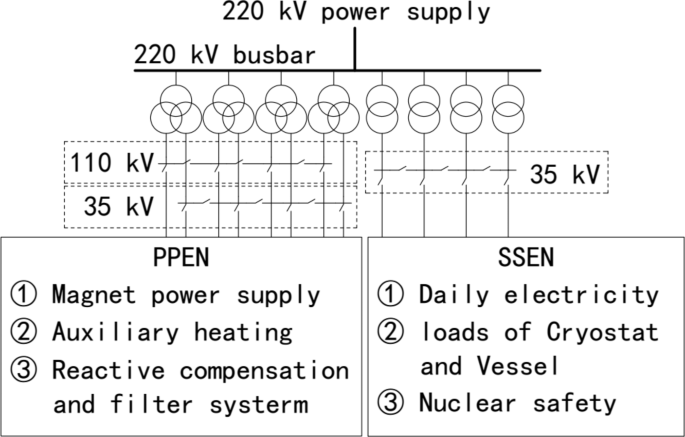
Starting from the functional requirements of various loads in CFETR, we establish the basic framework of the substation. The numbers and types of loads in CFETR are numerous and complex. According to the characteristics of loads, they are mainly divided into pulsed power electric network (PPEN) and steady state electric network (SSEN). PPEN has strong volatility, mainly including magnet power supply and auxiliary heating power supply; SSEN mainly refers to the continuous loads. In addition to the normal power consumption, SSEN mainly includes various motors in the vacuum and cryostat systems, the daily consumption loads, and the loads involving nuclear safety.
According to preliminary statistics, the active power of PPEN can reach 600 MW, the reactive power can reach 185 Mvar; the active power of SSEN is 200 MW, and the reactive power is 65 Mvar. The power factor at the common point where the two networks are connected is above 0.95. At full load operation, CFETR requires its bus short-circuit capacity to be no less than 13,500 MVA. However, since the magnet power supply, auxiliary heating, and current driving do not simultaneously reach peak power, the requirement for bus short-circuit capacity can be appropriately reduced.
According to the situation of the 500 kV substation around the CFETR, two 220 kV lines will be provided for power supply. The double bundled conductors with steel lightning conductor are used for input. The length of the line is estimated as 15 km. Four three-winding transformers supply PPEN, transformers and other equipments will reduce the voltage of 220 kV to 110 kV and 35 kV, respectively, and provide power to the 110 kV and the 35 kV busbar. Four double-winding transformers supply SSEN, transformers and other equipments will reduce the voltage of 220 kV to 35 kV, and provide power to the 35 kV busbar. The framework of substation in CFETR is shown in Fig. 1.
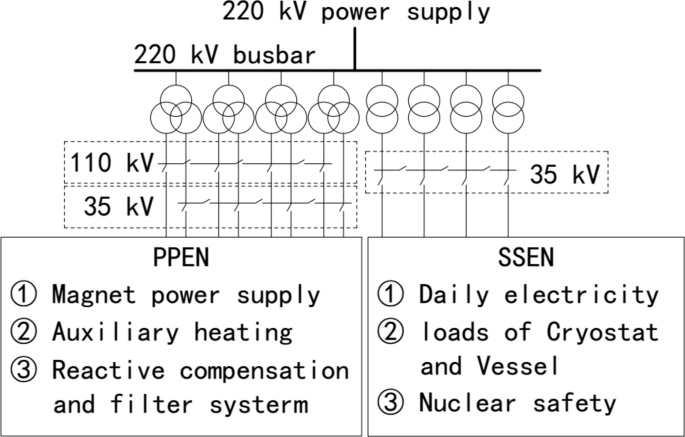
Configuration of 220 kV substation in CFETR.
The three phase short-circuit capacity of the electricity network is is 12,000 MVA, and the single phase short-circuit capacity is 10,500 MVA. The parameters of transformers are shown in Table 1 below. Each transformer operates separately.
Calculations of short-circuit
In this section, the values of various short-circuit currents at different positions are calculated, and finally the maximum fault current following into the ground is analyzed. Short circuit is a serious fault of power system. The possible types of short circuit include three phase short-circuit, two phase short-circuit, two phase grounding fault and single phase grounding fault 10. Three phase short-circuit is symmetrical, and other types of short circuit are asymmetrical. In this paper, the positive sequence equivalent rule is used to reduce all asymmetric short circuits to symmetric short circuit, so it is necessary to make positive sequence, negative sequence and zero sequence equivalent circuits of the substation.
Calculate the short-circuit currents at different locations in PPEN. If the reference power of the system is 100 MV•A and the reference voltage UB = Uav (average rated voltage), the reference current at different sides is:
$$\:{\text{I}}_{\text{B}}\text{}\text{=}\text{}\frac{{\text{S}}_{\text{B}}}{\sqrt{\text{3}}\text{}{\text{U}}_{\text{B}}}$$
(1)
Calculate the per unit impedance of each element. The rated frequency of power system is 50 Hz. The overhead bundled transmission line is horizontally arranged, and the line impedance is 11:
$$\:\text{x}\text{}\text{=}\text{}\text{0.1445}\frac{\text{1.26D}}{\sqrt{{\text{D}}_{\text{s}}\text{d}}}$$
(2)
D is the phase spacing of transmission line, which is 8 m; d is the spacing of bundled conductors, which is 400 mm; Ds is the geometric mean distance of the conductor, which is 15.12 mm. According to the above formula, the impedance of the transmission line is 0.31 Ω/km.
Convert the nominal value of impedance to the per unit value, and the positive sequence impedance is equal to the negative sequence impedance:
$$\:{\text{X}}_{\text{L}\left(\text{1}\right)\text{*}}\text{}\text{=}{\text{}\text{X}}_{\text{L}\left(\text{2}\right)\text{*}}\text{}\text{=}\text{}\text{x}\text{}\text{l}\text{}\frac{{\text{S}}_{\text{B}}}{{\text{U}}_{\text{B}}^{\text{2}}}$$
(3)
Where l is the line length equal to 15 km, the line is located at the 220 kV side, calculated by the above formula: XL(1)* = XL(2)* = 0.00879. For overhead lines with grounding conductors, the zero sequence impedance is approximately three times the positive sequence impedance.
Since the transformers have the same model and operate separately, the parameters of one transformer are calculated in combination with Table 1. For each winding of the transformer, the per unit values of the positive and negative sequence impedances are the same 12:
$$X_{Ti(1)\ast}=X_{Ti(2)\ast}=\frac{U_{Si}\%}{100}\times\frac{U_N^2}{S_N}\times\frac{S_B}{U_B^2}\times10^3(i=1,2,3)$$
(4)
UN is the rated voltage of each winding; SN is the rated capacity of each winding; UB is the reference voltage, that is the average rated voltage on each side; SB is the reference power of the whole system. Use Eq. (3) and Eq. (4) to calculate the per unit impedance of each winding: XT1(1)* = XT1(2)* = 0.0275, XT2(1)* = XT2(2)* = 0, XT3(1)* = XT3(2)* = 0.035. For the three-winding transformer without balancing coil, the zero sequence impedance of each winding is close to the positive sequence impedance value 13, and the approximate value of this project is: XT1(0)* = XT1(1)* = 0.0275, XT2(0)* = XT2(1)* = 0. As the low-voltage winding is connected in a triangle way, the zero sequence potential only forms a circulating current and is not connected to the external circuit, so there is no zero sequence impedance. Considering that the positive and negative sequence impedance of the power network is equal to 0.00833 and the zero sequence impedance is equal to 0.00952, the equivalent diagram of each sequence is drawn as shown in Fig. 2. Fault points are set at 220 kV, 110 kV and 35 kV buses respectively.
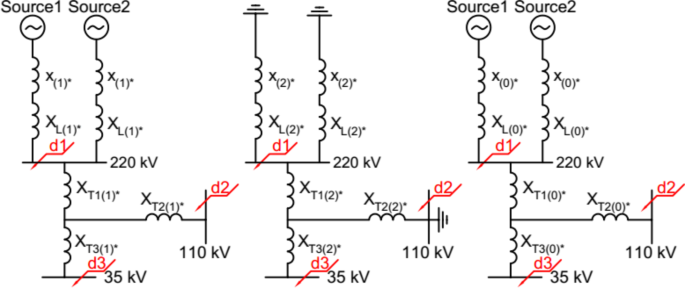
Equivalent diagram of each sequence of PPEN.
The transformers in SSEN have the same model and operate separately. According to Table 1, the parameters of one transformer are calculated. The per unit impedance of the two windings converted to the primary side is:
$$X_{T(1)\ast}=X_{T(2)\ast}=\frac{U_X\%}{100}\times\frac{U_N^2}{S_N}\times\frac{S_B}{U_B^2}\times10^3$$
(5)
Where, \(\:{\text{U}}_{\text{X}}{\%}\) is the short-circuit voltage of two-winding transformer; \(\:{\text{U}}_{\text{N}}\) is the rated voltage of the primary winding; SN is the rated capacity of the transformer; UB is the reference voltage, i.e. the average rated voltage; SB is the reference power of the power system. The per unit impedances are calculated from the above formula: \(\:\:{\text{X}}_{\text{T}\left(\text{1}\right)\text{*}}\text{}\text{=}{\text{}\text{X}}_{\text{T}\left(\text{2}\right)\text{*}}\text{}\text{=}\text{}\text{0.112}\), zero sequence impedance can be taken as: \(\:\:{\text{X}}_{\text{T}\left(\text{0}\right)\text{*}}\text{}\text{=}\text{}\text{0.112}\). The equivalent diagram of each sequence of SSEN is drawn as shown in Fig. 3 below.
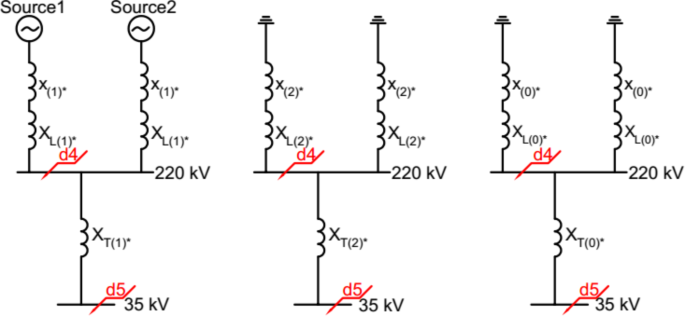
Equivalent diagram of each sequence of SSEN.
The positive sequence (Xff(1)), negative sequence (Xff(2)) and zero sequence impedance (Xff(0)) of each point are calculated according to the connection impedance at the fault point in Figs. 2 and 3. The calculation results are shown in Table 2 below.
The positive sequence equivalent rule is used to calculate three-phase short circuit current I(3), two-phase grounding fault current I(1,1), two-phase short circuit current I(2), single-phase grounding fault current I(1) respectively 14. The positive sequence component of asymmetric short circuit can be calculated as follows:
$$\:\text{I}_\text{fa(1)}^{\text{(n)}}{=}\frac{\text{U}_\text{f}^{0}}{\text{(}{{X}}_{ff(1)}\text{+}\text{X}_{\triangle}^{\text{(n)}}\text{)}}\:\:{\text{I}}_\text{B}$$
(6)
\(\:{\text{I}}_{\text{fa(1)}}^{\text{(n)}}\) is the positive sequence component of various asymmetric short circuit currents, f represents the fault point, and a represents the single phase current; \(\:{\text{U}}_{\text{f}}^{\text{0}}\) is the normal voltage at the fault point before short circuit; \(X_{ff(1)}\) is the positive sequence impedance at the fault point; \(X_\triangle^{\left(n\right)}\) is the additional impedance, and the superscript (n) represents the type of short circuit; \(\:{\text{I}}_{\text{B}}\) is the reference current at the fault point, determined by Eq. (1). The absolute value of various short circuit currents is proportional to the absolute value of its positive sequence component, namely:
$$\:{\text{I}}_{\text{f}}^{\text{(n)}}\text{}\text{=}\text{}{\text{}\text{m}}^{\text{(n)}}\:{\text{I}}_{\text{fa(1)}}^{\text{(n)}}$$
(7)
Where, \(\:{\text{m}}^{\text{(n)}}\) is the proportional coefficient, and its value varies according to the type of short circuit. See Table 3 below for additional impedance (\(X_\triangle^{\left(n\right)}\)) and proportional coefficient (\(\:{\text{m}}^{\text{(n)}}\)) of various short circuits.
The results of the absolute values of various short circuit currents are shown in Table 4 below.
It can be seen from the results in Table 4 that the maximum short circuit current occurs when the 220 kV bus bar in PPEN is three-phase grounded, namely: Ik.max=\(I_{d1}^{(3)}\) =29.32 kA . The flow direction of fault current is analyzed below. The requirements for grounding resistance of effective grounding system shall comply with 15:
$$\:R\leq\frac{\text{2000}}{{\text{I}}_\text{G}}$$
(8)
R is the maximum grounding resistance considering seasonal variation; IG is the effective value of the maximum asymmetric fault current following into the ground through the grounding grid.
When a grounding fault occurs in the substation, part of the short circuit current passes through the grounding conductor connected to the power network, so the current following into the ground is not equal to the short circuit current at the fault point. The symmetrical fault current following into the ground can be calculated according to the following formula 16:
$$I_g=(I_{k.max}-I_n)\times S_{f1}$$
(9)
Ik.max is the maximum effective value of symmetrical fault current; In is the current flowing through the neutral point; Sf1 is the shunt factor, which is taken as 0.5.
The key to solving the symmetrical fault current following into the ground is to calculate the current flowing through the neutral point 5:
$$I_n=\frac{x_{(0)\ast}}{X_{T1(0)\ast}+x_{(0)\ast}}I_{d1}^{(3)}$$
(10)
Use Eq. (9) and Eq. (10) to obtain the symmetrical fault current following into the ground: Ig = 10.89 kA. The effective value of the asymmetric fault current following into the ground is calculated according to the following formula 17:
$$\:\\I_G=D_f\times l_g$$
(11)
Df is the attenuation coefficient, which is calculated as follows 14:
$$\:{\text{D}}_{\text{f}}\text{}\text{=}\text{}\sqrt{\text{1}\text{}\text{+}\text{}\frac{{\text{T}}_{\text{a}}}{{\text{t}}_{\text{f}}}\text{}\text{[1}\text{}\text{-}\text{}\text{exp(-2}\text{}{\text{t}}_{\text{f}\text{}}\text{}\text{/}\text{}{\text{T}}_{\text{a}}\text{)]}}$$
(12)
Ta is the time constant of DC offset component, Ta = X / (ω R); The ratio of X/R at the fault point is 40. tf is the duration of grounding fault, taking 0.6 s and substituting Eq. (12) to get Df. Maximum value of asymmetric grounding fault current calculated from Eq. (11) is 11.99 kA. The IG is substituted Eq. (8) to obtain the range of grounding resistance: R < 0.167 Ω. The requirement value of grounding resistance is one of the bases for the design of grounding grid.